第三讲 完全信息动态博弈
3.1 扩展式博弈
扩展式博弈(extensive form)的要素:
- 博弈的参与人
- 参与人的决策顺序
- 参与人的行动空间 :每次决策参与人有什么选择
- 参与人的信息集 :每次行动参与人知道什么
- 参与人的支付函数 ;是所有参与人策略的函数
为了描述扩展式博弈的五要素,我们可以用博弈树(game tree)来表述。
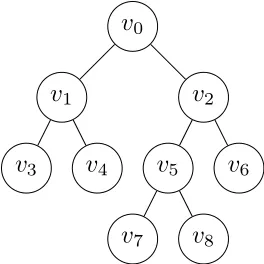
为初始结, 为决策结, 为终点结。
完全(complete)且完美(perfect)信息:在博弈进行的每一步当中,要选择行动的参与人知道这一步之前的整个过程;
每一条棱都表示参与人的一个行动; 每个节点最多只能有一个父节点; 并不要求每个链条都要有所有的参与人;
- 完美(perfect)信息:处于完美信息环境的参与人,都知道决策链条的历史信息。如果一个链条(贯序博弈)的每个决策节都是单节信息集,那么这个博弈就是完美信息博弈;
3.2 信息集
信息集(information set):满足以下三个条件的决策节的集合,
- 信息集中每个决策节都属于同一个参与人;
- 参与人无法区分同一个信息集的决策节;
- 参与人在每个信息集中都有相同的行动空间;
3.3 策略与行动
- 行动(Action):每一个决策节参与人决策的具体选择;
- 策略(Strategy):一个完整的计划,它明确了参与人所有可能遇到的情况的行动选择(每个信息集的决策节中选择的行动),例如性别战中,女生后手的策略是{足球芭蕾,…},这里的足球芭蕾的意思是女生面对男生的不同选择,分别采取足球和芭蕾两个选择;
再同时的静态博弈决策中,行动即策略;但在动态博弈中,策略与行动不等价,不同信息集下所能采取的行动是不同的,而所有的信息集下所能采取的所有行动的加总,则是策略;
- 纯策略:动态博弈的纯策略描述的是博弈中的一个完备的计划,它描述了参与人 在他的每一个信息集中将会选择的纯行动;
- 混合策略:在纯策略的基础上进行概率化、随机化;
- 行为策略(behavioral strategy):对纯策略的每一个信息集进行独立的概率化、随机化;
对于完美信息博弈,混合策略和行为策略是等价的;
3.4 扩展式的标准式表达
- 通过将扩展式的纯策略集当作标准式的纯策略集来使用,从而将扩展式博弈转化为标准式博弈;
- 每一个扩展式对应唯一一个标准式,反过来不成立;
- 通过转化可以帮助我们找到纳什均衡;
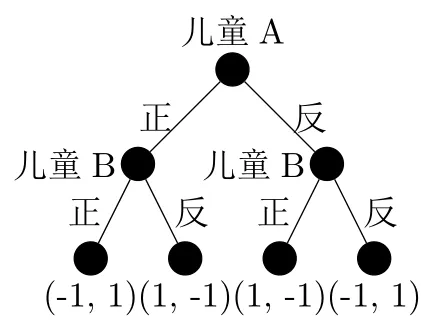
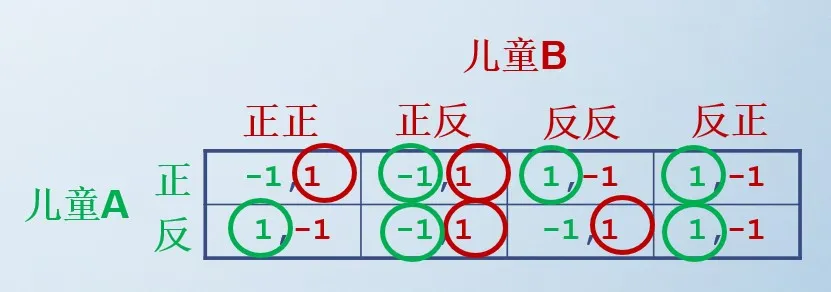
例子 1:动态猜字游戏的标准式
- 儿童 A 的策略集:(正, 反)
- 儿童 B 的策略集:(正正,正反,反正,反反)
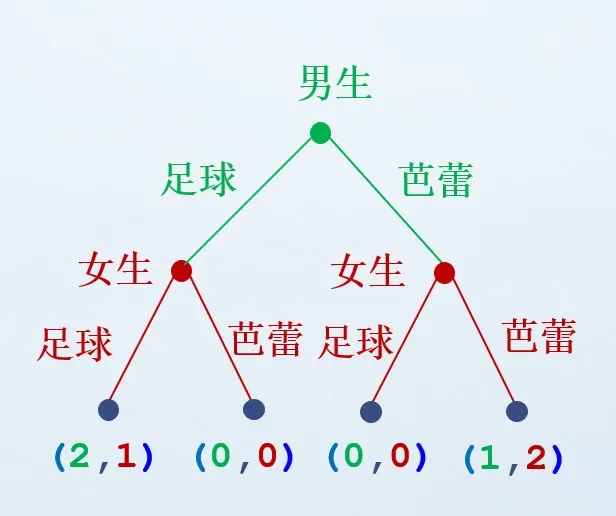
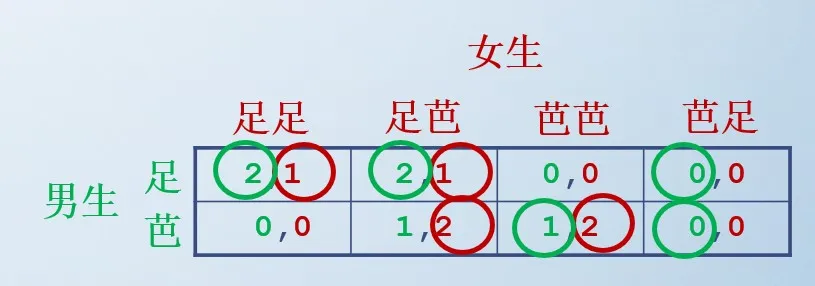
例子 2:动态性别战的标准式
- 男生的策略集:{足球,芭蕾}
- 女生的策略集:{足球足球,足球芭蕾,芭蕾芭蕾,芭蕾足球}
3.5 子博弈
在动态性别战中,Nash 均衡有(足球,足球足球)、(足球,足球芭蕾)、(芭蕾,芭蕾芭蕾),但是男生是先手,他没有理由选择主动选择芭蕾,所以均衡(芭蕾,芭蕾芭蕾)看起来并不合理;
我们将引入更严格的均衡概念以移除不合理的 Nash 均衡;
- 子博弈:当博弈进行到某点时,前面整个博弈的进行过程对所有的参与人而言都是共同知识,从该点开始的部分博弈称之为原博弈的子博弈;
扩展式博弈的子博弈需要满足一下三个条件:
- 始于博弈树中的单节信息集的决策节(不包括初始节);
- 包括博弈树中从该决策节开始的所有后续节(决策节和终点节);
- 没有对任何信息集形成分割。(如果信息集的一个决策节包含在子博弈中,则这个信息集中的其他决策节也必须在这个子博弈中);
子博弈精炼 Nash 博弈
-
如果博弈参与人的策略组合在每一个子博弈中都构成 Nash 均衡,则称子博弈精炼(subgame perfect)Nash 均衡
-
子博弈精炼 Nash 均衡存在性:在任何有限参与人、每个参与人的可行策略集有限的博弈中,都存在子博弈精炼 Nash 均衡,包括混合策略。
ps. 子博弈精炼 Nash 均衡是更强的 Nash 均衡,所以当某(对整体而言)Nash 均衡在子博弈中不是 Nash 均衡那该均衡就不是子博弈精炼均衡;
3.6 逆向归纳法
- 对于有限的完全且完美信息动态博弈,我们可以使用 逆向归纳法(backward induction) 求解子博弈精炼 Nash 均衡。
- 逆向归纳法:从那些直接与博弈终点相连接的决策节开始,寻找该决策节上参与人的最优选择;然后,退到上一层的决策节,寻找其参与者的最优选择;如此类推,直到初始节,即最高层次的子博弈。
例子 1:动态性别战的逆向归纳

- 在第二阶段,如果女生观察到男生在第一阶段选择足球,则其应该选择足球。反之,如果男生在第一阶段选择芭蕾,则女生会选择芭蕾。
- 回到第一阶段,根据女生第二阶段的选择,男生的最优选择是足球。
- 子博弈完美 Nash 均衡:(足球,足球芭蕾)
例子 2:Stackelberg 垄断模型
- 参与人:企业 1、2
- 行动顺序:企业 1 先选择,企业 2 后选择
- 行动空间:产量,
- 信息集:完全完美信息,企业 2 可以观察企业 1 的选择
- 支付函数:市场价格
解法: 从企业 2 的子博弈出发,求出企业 2 对于企业 1 的最优反应:
最优反应函数:
企业 1 在知道企业 2 会选择最优反应的基础上选择产量:
得到逆向归纳解:
3.7 逆向归纳法的适用范围
-
不完美信息博弈不适用:逆向归纳法需要分辨终点节前面的最后参与人集合,然后最大化这个阶段的支付函数,不完美信息集无法确定上家选了什么,所以无法写出最大化的式子;
-
无限次重复博弈不适用。
3.8 不完美信息博弈的逆向归纳
- 如果遇到非单节信息集就跳过先,继续向上直到遇到一个单节信息集;
- 然后同时考虑单节信息集行动的参与人的选择,以及被忽略的非单节信息集的参与人的选择;(相当于假定他们同时行动)
- 此外,还能将非单节信息集当作完全信息博弈来处理;
例子:不完美信息进入障碍博弈
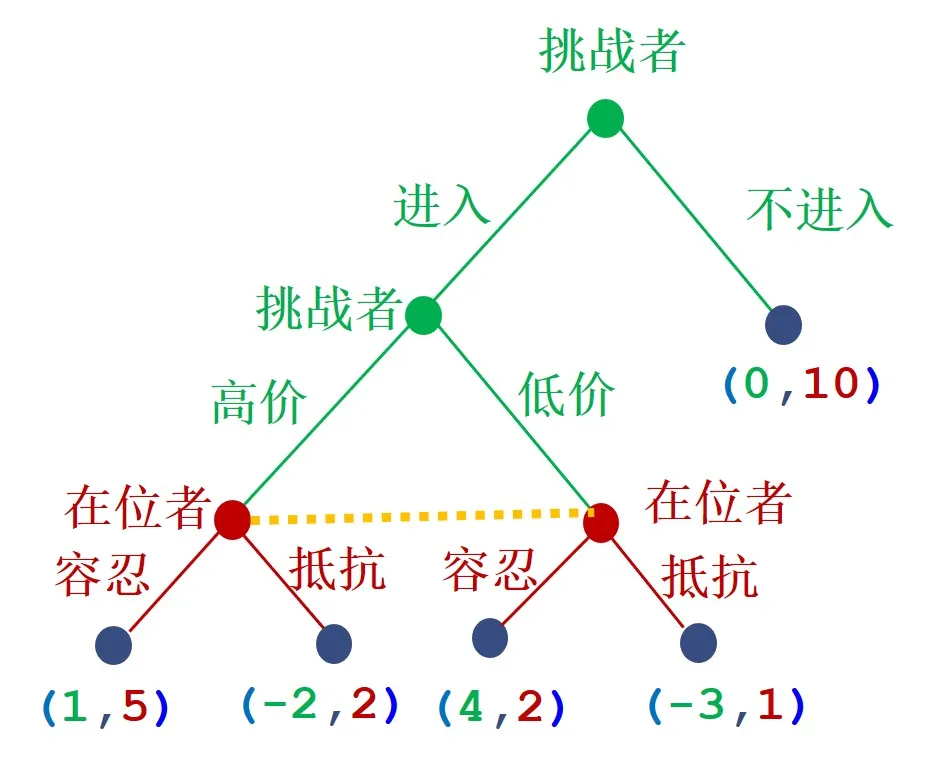
该博弈存在一个子博弈,该子博弈由于不完美信息集的存在,我们可以将其看作完全信息静态博弈来求解 Nash 均衡,解得 Nash 纯策略均衡为:(低价,容忍);
回到上一层博弈,初始节挑战者将选择进入市场(进入市场的均衡比不进入市场的支付要高),所以子博弈完美 Nash 均衡为(低价,容忍);
3.9 重复博弈
-
重复博弈(repeated game):是一个特殊的多阶段博弈,在这个博弈中的每一个阶段都重复着同一个阶段博弈。分为重复有限和重复无限博弈;
-
有限重复博弈指同一个阶段博弈重复有限次。给定阶段博弈 ,令 表示 重复 次的有限重复博弈,其中 是参与人的贴现因子。在下一阶段博弈开始前,所以之前的博弈可被观察, 的收益为 T 次阶段博弈收益的现值相加。
-
无限重复博弈 ,指阶段博弈 G 将无限次重复进行,并且每一阶段都是可观测的。
-
有限重复博弈
-
若阶段博弈 具有唯一的子博弈精炼 Nash 均衡:则该有限重复博弈拥有唯一的 Nash 均衡(同一阶段重复这个唯一的子博弈精炼均衡);
-
若阶段博弈 存在多个 Nash 均衡时:有限重复博弈有可能存在均衡,但不是各阶段 Nash 均衡的叠加;
-
折现因子的概念:子博弈的支付和父博弈的支付的加权和的权数;
例子:阶段博弈出现多个均衡的情况
折现因子 ; 考虑以下博弈重复两阶段的的情况:
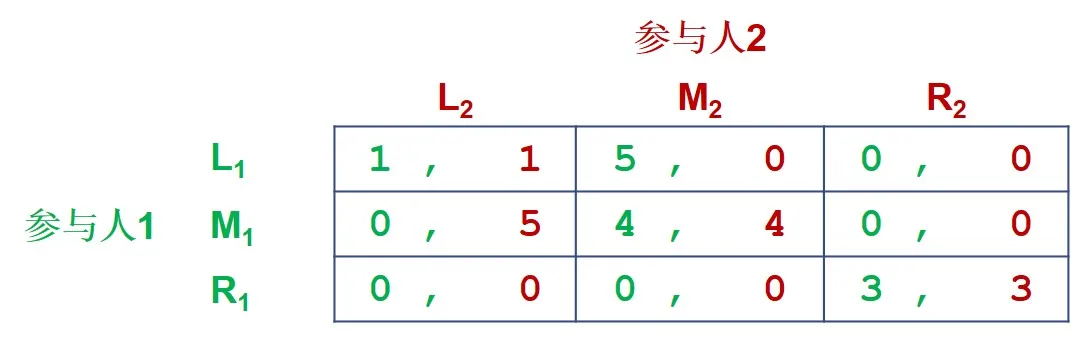
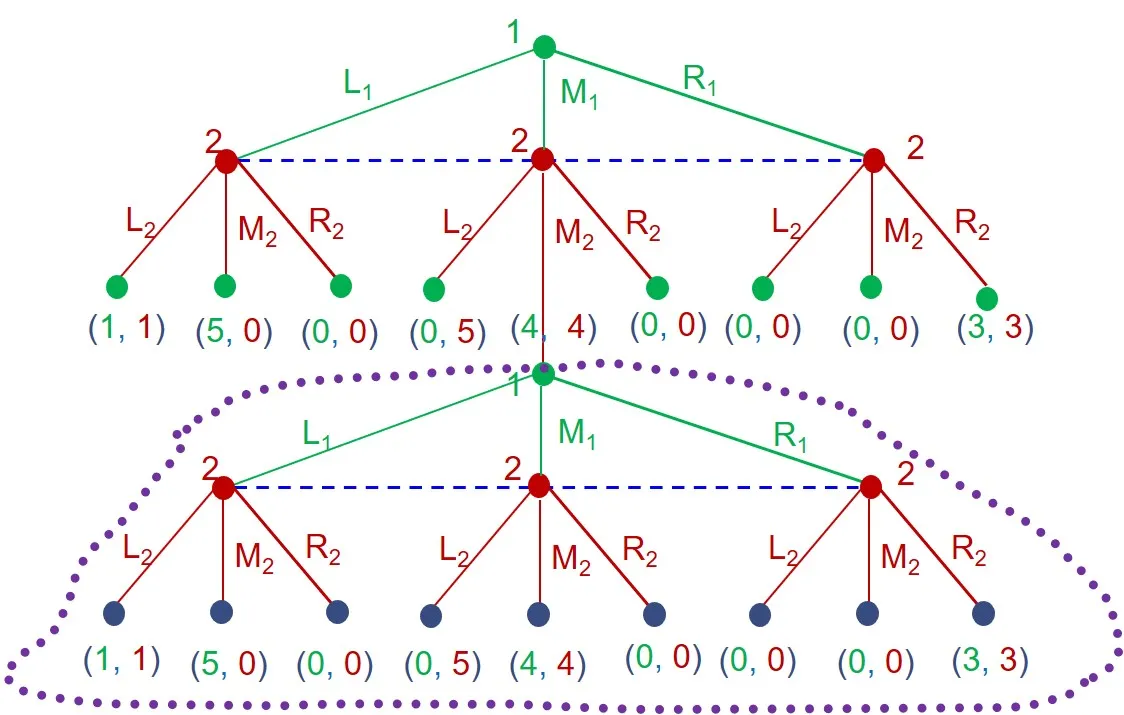
考虑一个策略组合: 不是说这个博弈就是均衡博弈; 可以看到这个策略组合在第二阶段构成一个 Nash 均衡; 现在考察是否构成整个博弈的 Nash 均衡; 根据这个策略组合,通过加权和的计算得到下表;
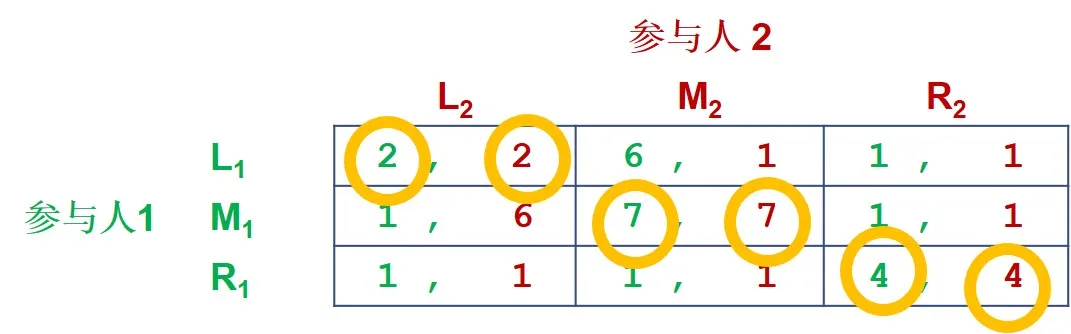
可以看到该策略组合的确是整个博弈的 Nash 均衡;
注:这里并不是在解一个 Nash 均衡,而是在验证一个策略集是否是整体博弈的 Nash 均衡解;
无限重复博弈
-
对于无限重复博弈,即使阶段博弈有唯一的 Nash 均衡,也可能存在子博弈精炼均衡,其中没有一个阶段的结果是 的 Nash 均衡;
-
令 为一个有限的完全信息静态博弈,令 表示 的一个 Nash 均衡支付, 表示其他可行支付,如果对于每一个参与人 有,且 足够接近于 1,则无限重复博弈 存在一个子博弈精炼 Nash 均衡,其每阶段的平均支付达到 ;
-
在无限重复博弈中,只有参与人有足够的耐心(δ 足够接近于 1),就总存在策略使得合作称为可能。
-
一个常用的策略是触发策略(trigger strategy):如果没有人选择不合作,合作将一直进行下去;一旦有人选择不合作,就会触发其后所有阶段都不再合作。(触发条件是需要计算的,结合触发前后支付函数的变化,通过控制参数,保证触发策略不会被打破)