第二讲 完全信息静态博弈

第二讲 完全信息静态博弈

主要内容：

• 标准式（策略式）博弈
• 重复剔除严格劣策略
• Nash 均衡
• 混合策略

什么是完全信息静态博弈？

• 静态博弈：每个参与人同时相互独立地决策，或决策有先后，但后决策者不知先决策者所采取的行动；
• 完全信息：参与人所有可能的行动、所有可能的结果、所有可能行动与可能结果的联系、以及每个参与人的偏好都被所有参与人知道；

标准式博弈

• 一个标准式博弈应该包含一下要素：
  • 博弈的理性参与人：$i=1, 2, 3, ... n$
  • 每个参与人可供选择的行动集合：$A_1, A_2, ... A_n$
  • 针对所有参与人所选择的行动，每个参与人获得的支付。$u_i(a_1, a_2, ... a_n)$，对于所有 $a_1 \in A_1, a_2 \in A_2, a_3, a_n \in A_n$
• 在一个 $n$ 个参与人的标准式中，参与人的行动集合为$A_1, A_2, ... A_n$，支付函数为$u_1, ... u_n$，我们用 $G = \{n; a_1, ... a_n; u_1, ..., u_n\}$表示该博弈；
• 策略集 $S_i$ 表示参与人 $i$ 所有的策略。一个策略组合 $s_i = (s_1, s_2, ... s_n)$ 为 $S_i$ 的子集；

在完全信息博弈中，参与人的策略集就是行动集合； 标准式可以用矩阵表示两个人的有限策略博弈；

构建过程案例：囚徒困境

• 参与人：{囚犯 1、囚犯 2}
• 行动/策略：$A_1 = A_2 = S_1 = S_2 = \{$ 沉默 | 坦白 $\}$
• 支付：由两个参与人的行动决定.

$u_1($ 沉默 | 沉默 $)=-1$ , $u_1($ 沉默 | 坦白 $)=-9$ , $u_1($ 坦白 | 沉默 $)=0$ , $u_1($ 坦白 | 坦白 $)=-6$ $u_2($ 沉默 | 沉默 $)=-1$ , $u_2($ 沉默 | 坦白 $)=0$ , $u_2($ 坦白 | 沉默 $)=-9$ , $u_2($ 坦白 | 坦白 $)=-6$

博弈求解

• 解(solution)是分析博弈的方法：在参与人的某些理性假设下，对博弈的所有可能结果进行筛选，留下更有可能的结果；
• 均衡(equilibrium)是博弈经过特定求解过程筛选后所剩下的策略组合(strategy set)，一个博弈可能存在多个均衡；

解法一：重复剔除严格劣策略

• 占优策略：无论其他参与人如何选择，这个策略都比其他策略的支付函数要高，就叫做占优策略；
• 劣策略：相反，如果一个策略的支付函数始终不高于其他策略的支付函数，那么就是劣策略（其中，低于的策略叫严格劣策略）；

重复剔除严格劣策略的解法就是，通过剔除严格劣策略来将现有博弈转化为一个新的博弈，再对新的博弈重复上述过程，直到无法剔除为止，得到博弈的解； 对于离散型博弈，我们通常使用划线法剔除严格劣策略得到博弈的解； 缺陷：

• 重复剔除严格劣策略的前提是，所有的参与人都知道其他参与人是理性人且剔除的顺序都不影响最终结果；
• 只有存在严格劣策略时，才能剔除，并不是所有博弈都有严格劣策略，如性别战；

解法二：最优反应策略

• 最优反应策略(best response)：如果参与人 $i$ 的策略 $s_i$ 对其他参与人的策略 $s_{-i}=\{s_1, s_2, \dots s_{i-1}, s_{i+1}, \dots, s_n\}$ 有

那么我们说该策略 $s_i$ 为最优反应策略；

由于一个理性人总会对其他人选择的策略 $s_{-i}$ 选择自己的最优反应策略 $s_i$ 。因此博弈可以被转化为求解：

解出来的结果为：$\{s_i^*, s_{-i}^*\}$ Nash 均衡是一个策略组合，这个组合中每个参与人针对其他参与人的策略所选择的反应是最优反应，且每个参与人都不愿意独自离开选定的策略。 对于离散博弈，通常使用划线法选择相对占优策略的交集寻找 Nash 均衡解；

ps：一个博弈的 Nash 均衡解是剔除严格劣策略的解的子集；

连续型博弈

对于连续型博弈，不能使用划线法得到解。我们通常联系支付函数的一阶导数，另一阶导数为 0 得到最优反应策略；

例题 1

1. 中间选民：设有一批选民的政策倾向在一个单位区间从左（x = 0）至右(x = 1)均匀分布，为一个职位参加竞选的两个候选人同时选择其竞选的政策倾向（即在 x = 0 到 x = 1 中间的一个点）。选民观察候选人的选择，然后把票投给其政策倾向离自己最近的候选人。获得选票数量更多的候选人将获胜。如果两个候选人选择相同的政策倾向，则平分所得选票。如果两人获得选票数量相同，谁当选由掷硬币来决定。
2. n 个厂商的 Cournot 模型：假设在 Cournot 寡头垄断模型中有 n 个厂商。设 qi 为厂商 i 的产量，同时设 Q = q1 +…+qn 为总产量。设 P(Q)为市场出清价格（当需求为 Q 时），并假设反需求函数为 P(Q) = a – Q，这里 Q ≤ a。假设这些厂商都没有固定成本且产量为 qi 时生产成本为 cqi（所有的厂商都有相同的边际成本，同时假设 c < a）。

1. 中点选民： 参与人：候选人 $A$ , $B$ 行动：$A_1=S_1={x_1 }, A_2=S_2={x_2 }, 0≤x_1, x_2≤1$ 不妨设 $x_1≤x_2$, 支付： $u_1 (x_1, x_2 )= (x_1+x_2)/2$ $u_2 (x_1, x_2 )= 1-(x_1+x_2)/2.$ 为求得最优反应函数，我们需要求解： $\max \limits_{0≤x_1≤x_2}u_1 (x_1, x_2^*) = (x_1 + x_2^*)/2$ $\max \limits_{x_1≤x_2≤1}⁡u_2 (x_1^*, x_2 )=1-(x_1^*+x_2)/2$ 得到最优反应函数： $x_1^*=x_2^*$ $x_2^*=x_1^*$ 得到 Nash 均衡解$(x_1^*, x_2^* )$，且 $x_1^*=x_2^*$。而此时$u_1 (x_1^*, x_2^* )=u_2 (x_1^*, x_2^*)=x_2^*=1-x_2^*=1/2$ 所以最后均衡解为 $(1/2, 1/2)$.
2. N 个厂商的 Cournot 模型： 参与人：厂商 $1, 2, 3, \dots, n$ 行动：$A_i=S_i=q_i∈[0, a]$ 支付： $u_i (q_i )=P(Q)Q=(a-Q-c) q_i$ 对于企业 i 为求得最优反应函数，需要求解： $\max \limits_{0≤q_i≤a}⁡ u_i (q_i, q_{-1}^*) = (a-q_i - q_{-i}^* - c)q_i$ 得到最优反应函数： $q_i^*=(a-c-q_{-i}^*)/2$ 联立 n 个企业的最优反应函数求得 Nash 均衡为：$(q_1^*, q_2^*, \dots, q_n^*)$ 而 $Q^*=q_1^*+q_2^*+⋯+q_n^*$ 满足以下条件： $Q^* = n(a-c)/(n+1)$

混合策略均衡

有些博弈并没有纯策略的 Nash 均衡，比如猜字游戏，我们找不出绝对的最优策略，每个参与人最合理的做法便是随机选择策略，这种随机化选择策略的做法就是混合策略的思想；

由于引入了概率，于是我们便用分布函数来描述支付函数，参与人 $i$ 选择纯策略 $s_i$ 的支付函数表示为，其他参与人所选择策略的概率分布函数的期望（收益由他人的选择决定）

例题 2

1. 求解下述博弈的混合战略 Nash 均衡：

两个企业各有一个工作空缺，假设企业所给的工资不同：企业 $i$ 给出的工资为 $w_i$ ，这里$\dfrac{1}{2}w_1 < w_2 < 2w_1$。设想有两个工人，每人只能申请一份工作，两人同时决定是申请企业 1 的工作，还是向企业 2 申请。如果只有一个工人向一个企业申请，他就会得到这份工作；如果两个工人同时向一个企业申请工作，则企业随机选择一个工人，另一人就会失业（这时收益为 0）。

• 参与人：工人 1、2
• 行动：$A_1=A_2=\{w_1, w_2\}$
• 支付：

$u_1(w_1, w_1)=\dfrac{1}{2}w_1, \quad u_1(w_1, w_2)=w_1, \quad u_1(w_2, w_1)=w_2, \quad u_1(w_2, w_2)=\dfrac{1}{2}w_2$ $u_2(w_1, w_1)=\dfrac{1}{2}w_1, \quad u_2(w_1, w_2)=w_2, \quad u_2(w_2, w_1)=w_1, \quad u_2(w_2, w_2)=\dfrac{1}{2}w_2$

• 混合战略：
  • 工人 1 分别以概率 $r$ 和 $1-r$ 选择申请的公司 1、2；
  • 工人 2 分别以概率 $q$ 和 $1-q$ 选择申请的公司 1、2；
• 工人 1 的支付期望：
  • 选择企业 1：$\dfrac{1}{2}w_1q + w_1(1-q) = (1-\dfrac{1}{2}q)w_1$
  • 选择企业 2：$w_2q + \dfrac{1}{2}(1-q)w_2 = \dfrac{1}{2}(1+q)w_2$
• 工人 1 的最优反应函数：
  • 当 $q < \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，选择企业 1 ($r=1$)
  • 当 $q > \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，选择企业 2 ($r=0$)
  • 当 $q = \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，两种选择无差异 ($0 < r < 1$)

import matplotlib.pyplot as plt
plt.plot([0, 0.6, 0.6, 1], [1, 1, 0, 0])
plt.xlabel('q-label')
plt.ylabel('r-label')
plt.show()

• 工人 2 的支付期望：

• 选择企业 1：$\dfrac{1}{2}w_1r + w_1(1-r) = (1- \dfrac{1}{2} r) w_1$

• 选择企业 2：$w_2 r + \dfrac{1}{2} w_2 (1-r) = \dfrac{1}{2} (1+r) w_2$

• 工人 2 的最优反应函数：

  • 当 $r < \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，选择企业 1 ($q=1$)
  • 当 $r > \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，选择企业 2 ($q=0$)
  • 当 $r = \dfrac{2w_1 - w_2}{w_1 + w_2}$ 时，两种选择无差异 ($0 < q < 1$)

import matplotlib.pyplot as plt
fig, ax = plt.subplots()

ax.plot([0, 0.6, 0.6, 1], [1, 1, 0, 0])
ax.plot([0, 0, 1, 1], [1, 0.6, 0.6, 0])
fig.suptitle("r-q")
ax.grid(True, linestyle='-.')
ax.tick_params(labelcolor='r', labelsize='medium', width=3)
plt.xlabel('q-label')
plt.ylabel('r-label')
plt.show()

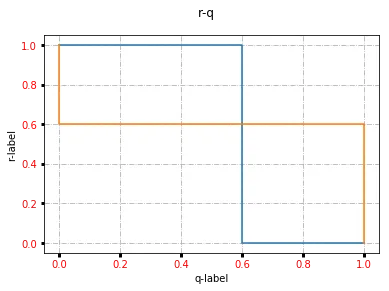
所以，混合策略均衡为($\dfrac{2w_1 - w_2}{w_1 + w_2}, \dfrac{2w_1 - w_2}{w_1 + w_2}$).

Nash 均衡存在性

在 $n$ 个参与人的标准式博弈 $G = \{N; (A_i); (u_i); \}$ 中，如果 $n$ 是有限的，且对于每个参与人 $i$ 的策略集 $S_i$ 也是有限的，则博弈存在至少一个 Nash 均衡，均衡也可能包含混合策略。