导数的应用

极值

绝对极值（最值）（最大、最小）

相对极值（局部）（ $\rightarrow f'(c)=0$ ）

临界点（ $\Leftrightarrow f'(c)=0或f(c)=0$ ）

极值相关定理

定理 1 连续函数的极值定理

对于在闭区间 $I$ 上的连续函数 $f(x)$ ，在某些点处能取到最大值 $M$ 和最小值 $m$ ，那么对于 $I$ 中的所有 $x$ ，都有 $m \le f(x) \le M$ 。（废话）
定理 2

在函数 $f$ 的定义域内点 $c$ 处取到局部最大值或局部最小值，点 $c$ 也存在导数，那么 $f'(c)=0$ 。

微分中值定理

定理 1 罗尔定理

定义在 $[a,b]$ 的连续可微函数 $f(x)$ ，如果 $f(a)=f(b)=0$ 那么至少有一个数 $c$ 使得 $f'(c)=0$
定理 2 微分中值定理

定义在 $[a,b]$ 上的连续可微函数 $f(x)$ ，那么 $(a,b)$ 内存在一点 c，使得 $\frac{f(b)-f(a)}{b-a}=f'(c)$

我们可以看到，罗尔定理其实是微分中值定理的特殊情况。

图形的形状

增减函数检验

定义检验
一阶导数正负检验

局部极值的检验
一阶导：

局部极小值， $f'(x)$ 从负变正
局部极大值， $f'(x)$ 从正变负
没有局部极值， $f'(x)$ 两边同号

二阶导：

$f'(c)=0$ 且 $f''(c) \gt 0$ ，那么 $f$ 在 $x=c$ 处取得极小值
$f'(c)=0$ 且 $f''(c) \lt 0$ ，那么 $f$ 在 $x=c$ 处取得极大值

凹性

凹向上， $y'' \gt 0$
凹向下， $y'' \lt 0$

拐点

凹性改变的点，叫做拐点。二阶导函数等于零，且一阶导函数有极大值或极小值的点是拐点。
但二阶导数等于零也不一定是拐点，二阶导数不存在也可能是拐点。

自治微分方程的图形解

自治微分方程

导数只是关于 y 的函数，我们称该方程为自治微分方程。

平衡点/静止点

使自治微分方程 $\dfrac{dy}{dx}=g(y)$ 等于零的 y 值，称之为平衡点或静止点。

相直线

是一条用来表示函数的高阶导数的正负性的数轴。

借助相直线，我们可以得到自洽微分方程的图形解（没有表达式，但知道解的函数大致图像）。

三个案例

冷却

假设环境摄氏温度为 $P$ ，汤的温度为 $H$ ，经过的时间为 $t$ ，我们还假设环境足够大，使得汤的温度对环境的影响忽略不计。根据牛顿的冷却定律有：

\frac{dH}{dt} = -k(H - P)

当 $H \gt P$ 时， $\dfrac{dH}{dt} \lt 0$ 。

经过求导之后，画出相直线。

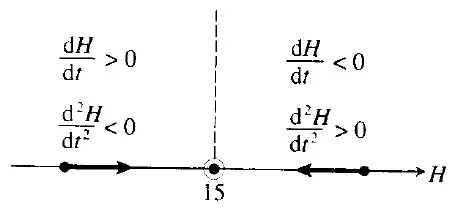
微分方程的图形解如图：

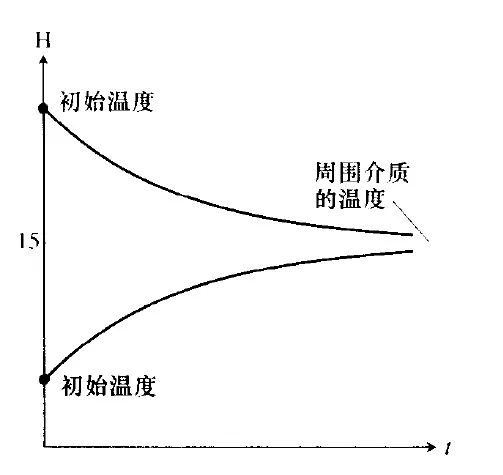
图中的 15 是一个稳定的平衡点，上下的两条直线都稳定朝 15 靠近。

分析有阻力时的落体

按照动量定理，我们有：

F=\frac{d}{dt} (mv) = m \frac{dv}{dt} + v \frac{dm}{dt} = m \frac{dv}{dt}

当物体在介质中下落时，往往会受到阻力，阻力往往与速度相关，这时得到的公式为：

F = F_g - F_v = m (g - kv), \newline a = g - \frac{kv}{m}.

当物体受到的合力 $F=0$ 时，速度便稳定下来，故稳定速度为 $v = \frac{mg}{k}$ 我们考察速度的变化过程：

\frac{d^2v}{dt^2} = \frac{d}{dt} (g - \frac{k}{m} v) = - \frac{k}{m} \frac{dv}{dt}

画出相直线：

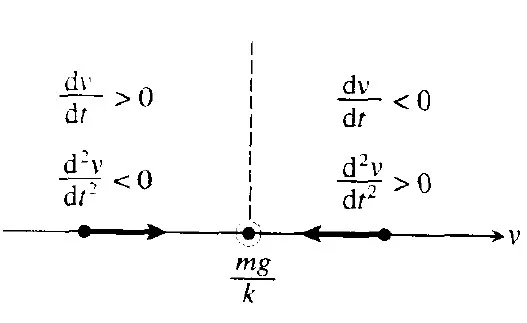
画出图形解：

阻力图形解

logistic 增长

假设 $P=P(t)$ 为某个种群的数目，在时间 $\Delta t$ 内，种群的增长率为 $k$ ，则种群数目为： $\frac{\Delta P}{\Delta t}=kP(t)$ $k \gt 0$ 是种群的增长率，对增长率进行假设：在自然界中，由于有限的资源，我们通常会假设一个极限种群或承载容量 $M$ ，资源变得短缺了，种族的增长率 $k$ 便会降低，

k = r(M-P)

$r$ 代表了增长率变化的速度，对 $k$ 进行代换得到：

\frac{dP}{dt} = r(M-P)P=rMP-rP^2

该模型称之为logistic 增长模型。

考察该模型的函数性态，我们对上述模型两边求导：

\frac{d^2P}{dt^2} = rM \frac{dP}{dt} - 2rP \frac{dP}{dt}=r \frac{dP}{dt} (M - 2P)

画出相直线得：

logistic 增长相直线

画出图形解：

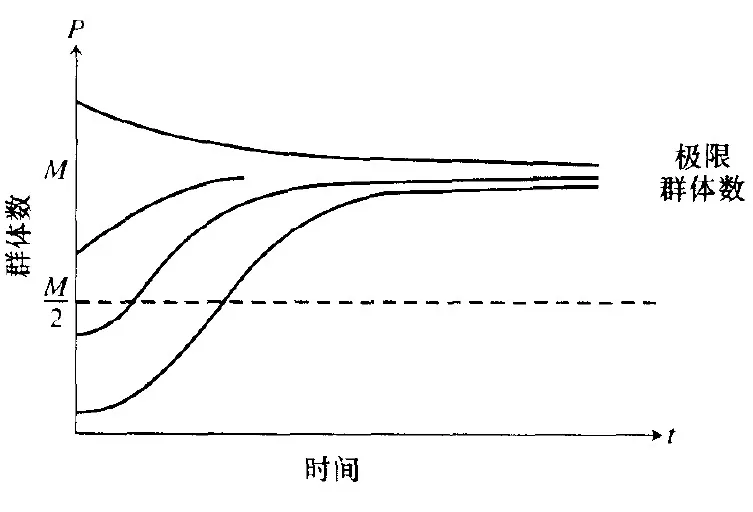
logistic 增长图形解

我们可以看到，拐点在 $\frac{M}{2}$ 位置处。

建模和最优化

求解最大-最小问题
1. 了解问题
2. 研制一个该问题的数学模型
3. 求该函数的定义域
4. 识别临界点和端点
5. 求解该数学模型
6. 对解进行解释

书中使用了 Fermat 原理和 Snell 定律来进行建模举例。

Fermat 原理：光在介质中传播永远以时间最短的路径传播。
Snell 定律：在介质之间相互传播的时候，入射角和折射角满足一定的关系：
$\frac{\sin \theta_1}{c_1} = \frac{\sin \theta_2}{c_2}$

线性化和微分

线性化

如果 $f$ 在 $x = a$ 可微，那么近似函数
$L(x) = f(a) + f'(a) (x - a)$
就是 $f$ 在 $a$ 的线性化 近似 $f(x) \approx L(x)$ 是 $f$ 在 $a$ 的标准线性近似，点 $a$ 就是线性中心。

微分

设 $y = f(x)$ 是一个可微函数，微分 $dx$ 是一个自变量。微分 $dy$ 是
$dy = f'(x)dx$
变量 $dy$ 永远是一个因变量，它既依赖于 $x$ ，又依赖 $dx$ .

根式函数和幂函数的线性化
$(1+x)^k \approx 1 + kx$
在 $x = 0$ 附近常用线性化
$\sin x \approx x ,\ \cos x = 1 ,\ \tan x \approx x$
绝对变化
- 估计变化 $\Delta f = f(a + dx) - f(a)$
- 实际变化 $df = f'(a)dx$
相对变化
- 估计的变化 $\frac{df}{f(a)}$
- 实际变化 $\frac{\Delta f}{f(a)}$

变化的敏感度

由 $df = f'(x)dx$ ，我们知道 $f'(x)$ 可以衡量 $f$ 对 $dx$ 的敏感程度。（这一点可能在多变量的情形下起作用）

微分变化估计实际变化的误差

估计误差

$\begin{aligned} \Delta f - df & = f(a + \Delta x) - f(a) - f'(a) \Delta x \\ & = \Delta x (\dfrac{f(a + \Delta x) - f(a)}{\Delta x} - f'(a)) \end{aligned}$
令 $\dfrac{f(a + \Delta x) - f(a)}{\Delta x} - f'(a) = \epsilon,$ 则上式 $= \Delta x \epsilon$ 当 $\Delta x \rightarrow 0$ 时， $\epsilon \rightarrow 0$ .

Newton 法

本节介绍一个求解根的方法：牛顿(Newton)法

Newton 法

通过切线的零点，确定下一条切线，再根据下一条切线的零点，确定再下一条切线…如此循环往复，最后得到要找的根。如下图：

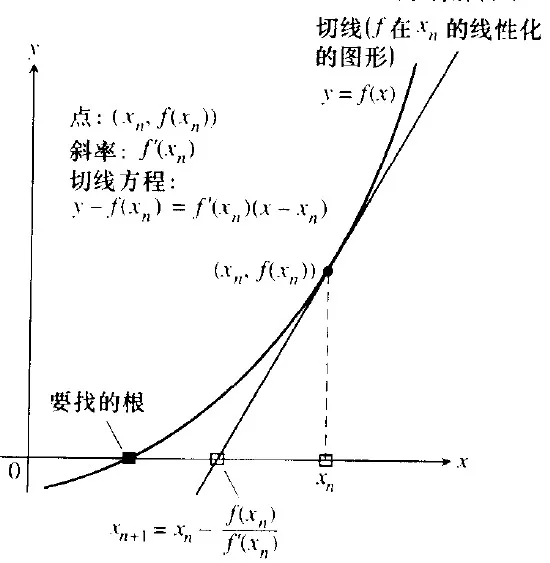
Newton 法由线性化可知，牛顿法代数上计算就是根据给定的 $x_0$ 求得 $f(x_0)$ 和 $f'(x_0)$ 再代入：
$x = x_n - \frac{f(x_n)}{f'(x_n)}$
然后循环以上步骤，直至 $x_n$ 收敛于某个固定的值（也可能不收敛，此时 $f(x)$ 无零点。

Newton 法失效的情况：

当 $f'(x_n) = 0$ 时，Newton 法就会停下来，这时便需要选择别的起点；
Newton 法有时会陷入无限循环，无法收敛。

求得的根不是想要的根的情况：

Newton 法不是想要的根

分形盆

我们使用 Newton 法解 $z^6 - 1 = 0$ ，我们根据不同的起始点，经过多次迭代之后得到如图：

这一个个盆形区域被称为分形盆，这六个分形盆他们分别导向这个复数方程的六个解 $1,-1, \pm \sqrt{3} / 2, \pm 1/2$