分组加密算法

分组加密算法

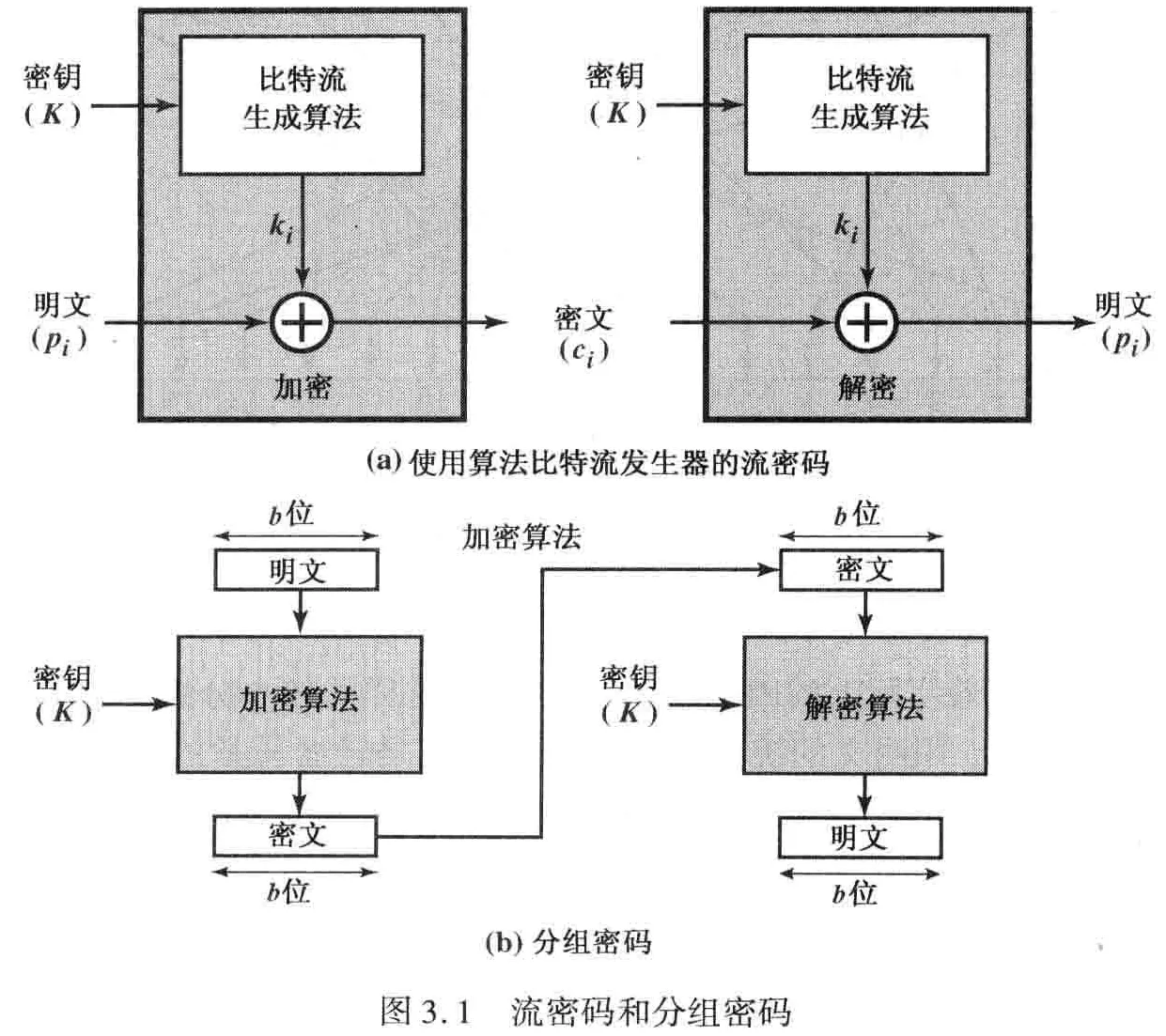
流密码 vs 分组密码

流密码一次加密一位或者一个字节

• Vigenere 密码
• 一次一密版本的 Vernam 密码

分组密码需要共享一对对称密钥，一次加密一个明文分组得到与明文等长的密文分组；

流密码面对的问题：

1. 通信双方的密钥流必须以某种安全、独立的方式共享。如果需要通信的数据流量很大，那么就难以保证安全；
2. 如果使用交换密钥 $K$ ，然后使用密钥 $K$ 和相应的密钥生成程序（位流发生器）生成密码学意义上可用的、强壮的密钥流。则可以解决以上的问题。

Feistel 密码结构的设计动机（这部分有问题，待修改）

• 可逆映射（非奇异变换）
• 不可逆映射（奇异变换）

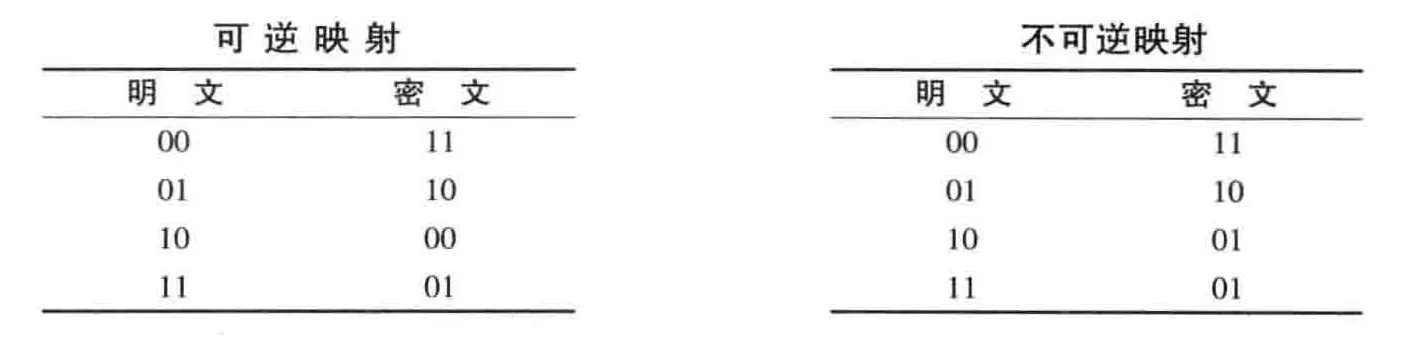
1. 分组密码需要同时满足加密和解密的需求，所以明文密文之间的映射必须可逆。意味着对 $n$ 位长的分组进行加密时，有 $2^n$ 种组合，我们的加解密算法需要满足有 $2^n$ 大的密文空间；
2. $n$ 需要充分大，并且允许明文和密文之间采用任意的可逆映射（变换）将明文的特征掩盖，否则就和传统的代替密码一样容易被统计方法破解；

Feistel 密码

混淆和扩散

混淆和扩散是区别于代替和置换的概念。

• 混淆：尽可能地使加密密钥和密文之间的统计关系变得复杂，使得发现密钥变得困难；
• 扩散：尽可能地使明文和密文之间的统计关系变得复杂，使得推导密钥变得困难；

DES

详见 DES 文章

雪崩效应：指的是明文微小的改变将引起密文的很多位改变，这有助于阻止攻击者猜测密钥或明文空间。

分组密码的工作模式

本质上，工作模式是用于增强密码算法或者使算法适应具体应用的技术。

电码本模式（ECB）

一次处理 $b$ 位明文，每次使用相同的密钥加密。

密码分组链接模式（CBC）

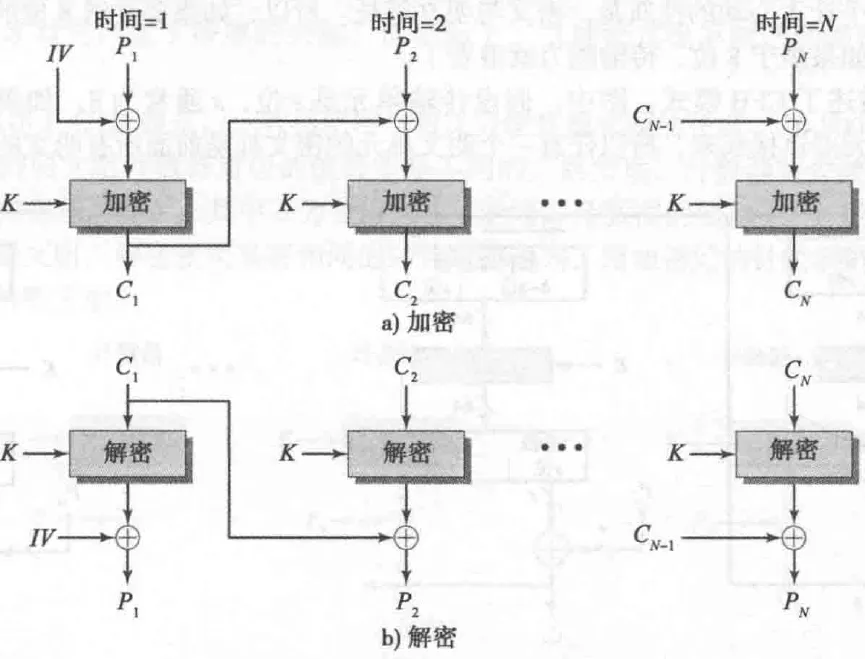
• 加密：

• 解密：

密码反馈（CFB）

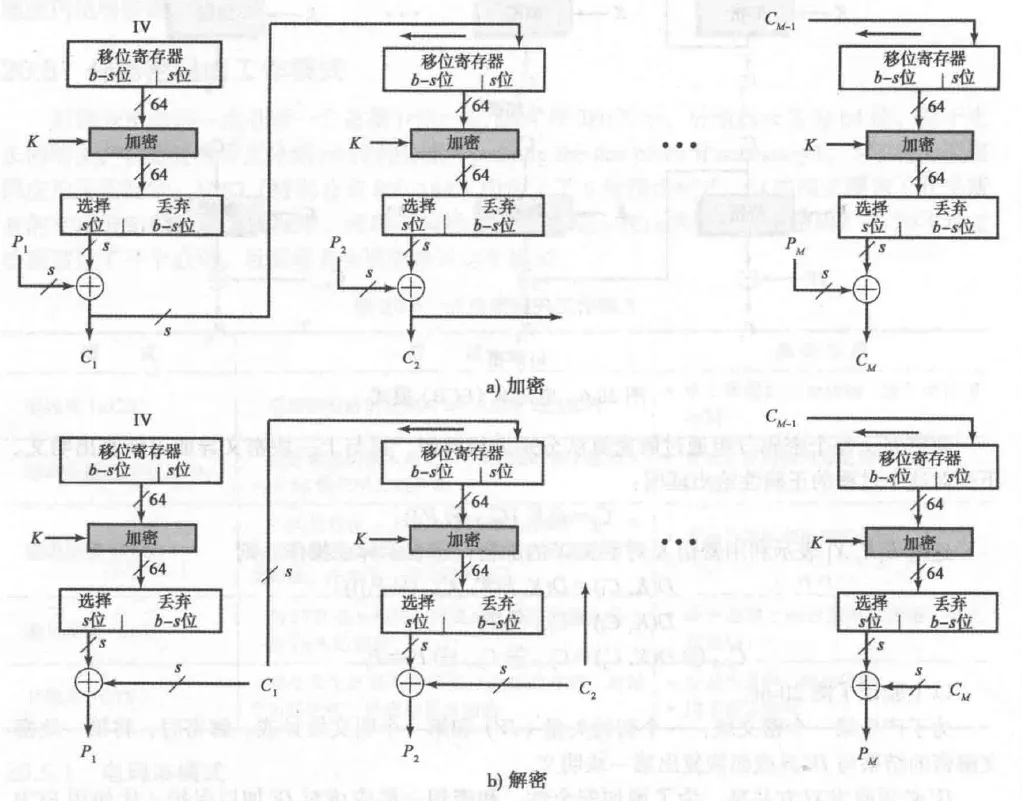
将任意分组密码转换为流密码。

• 加密：

• 解密：

输出反馈（OFB）

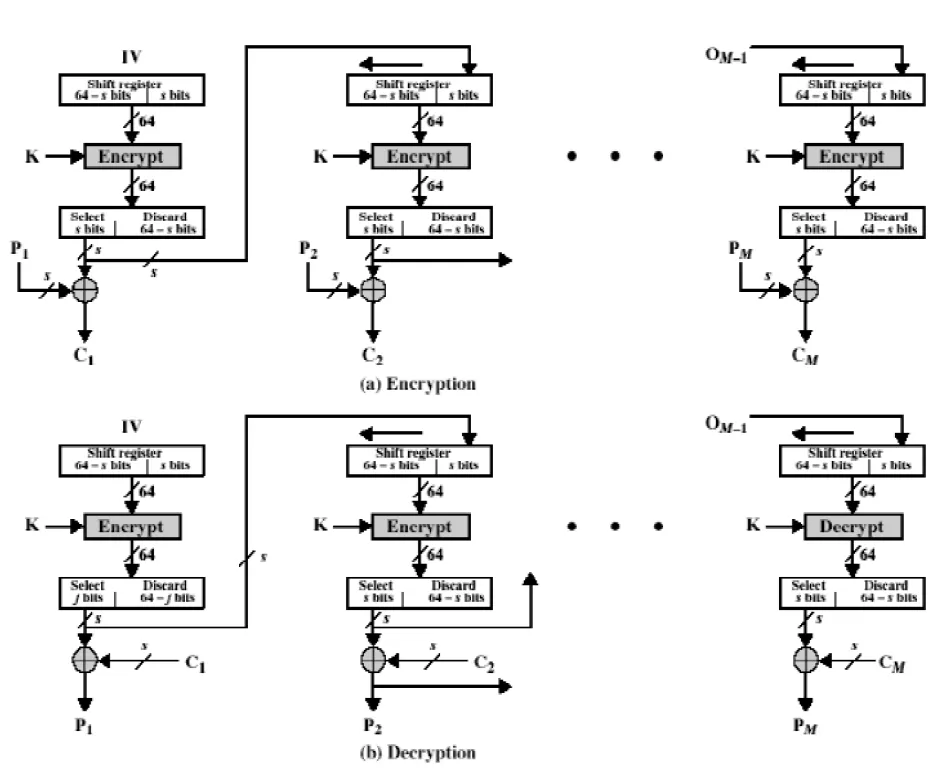
与密码反馈基本一致，加密算法的输入是上一次 DES 的输出。

计数器（CTR）

$C_n = P_n \oplus E(K, Counter)$

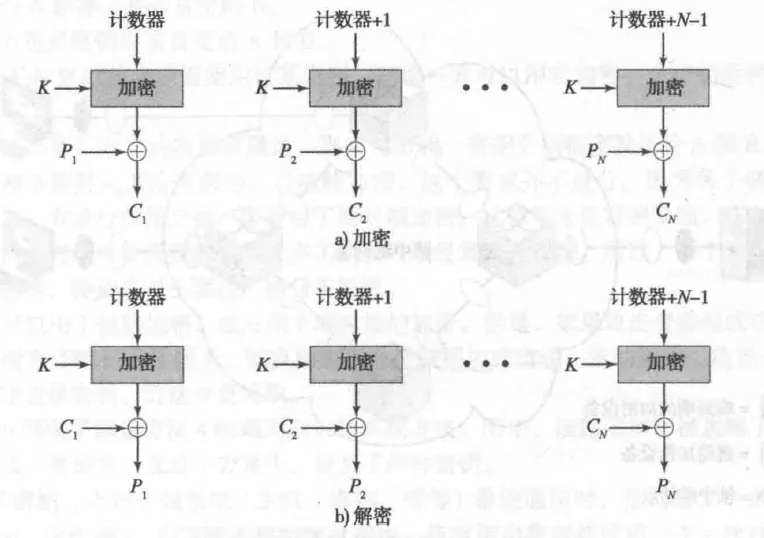
初始化一个计数器，当消息块逐渐增加，计数器也随之增加。再将计数器与明文异或，得到密文。
特点：可并行化、可预处理、不需要设计解密算法、随机访问……