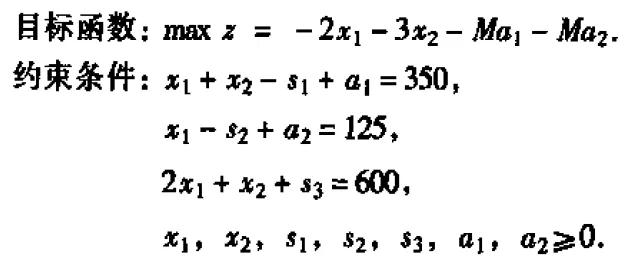运筹学算法

单纯形法

基本思路：
找出一个基本可行解 $\to$ 检验是否为最优解 $\to$ 更换基变量 $\to$ 迭代以上步骤

基于线性规划标准化后可以写成：(S 为松弛变量或者调整变量)

1. 基
   基$\boldsymbol{B}$是约束系数矩阵$\boldsymbol{A}$的非奇异子矩阵 (即$\boldsymbol{B}$是可逆矩阵，$\boldsymbol{|B|} \ne 0$)。 $\boldsymbol{B}$是$\boldsymbol{A}$中$m$个线性无关的列向量组成。
2. 基向量
   基$\boldsymbol{B}$中的一列为一个基向量。
3. 非基向量
   $\boldsymbol{A}$中除了基$\boldsymbol{B}$之外的向量为非基向量。
4. 基变量
   与基向量相对应的$x_i$。
5. 非基变量
   与非基变量相对应的$x_i$。

详细步骤：

1. 初始化线性规划模型；
2. 找出一个基，它是单位矩阵;
3. 用非基变量表示基变量，并令非基变量为 0，得出基本可行解;
4. 最优性检验，将目标函数中的基变量代换为非基变量，得到的 i 个系数为检验数， 当检验数都小于等于 0 时，说明得到最优解；
5. 若不是最优解，则进行基变换，将$\sigma_i$对应的$x_i$的基向量入基(基变量)， 对基变量$x_i$，将$\frac{b_j}{a_{ij}}$比值最小的确定为出基变量；
6. 再进行最优性检验，直至无最优解为止。

单纯形法的表格表示：

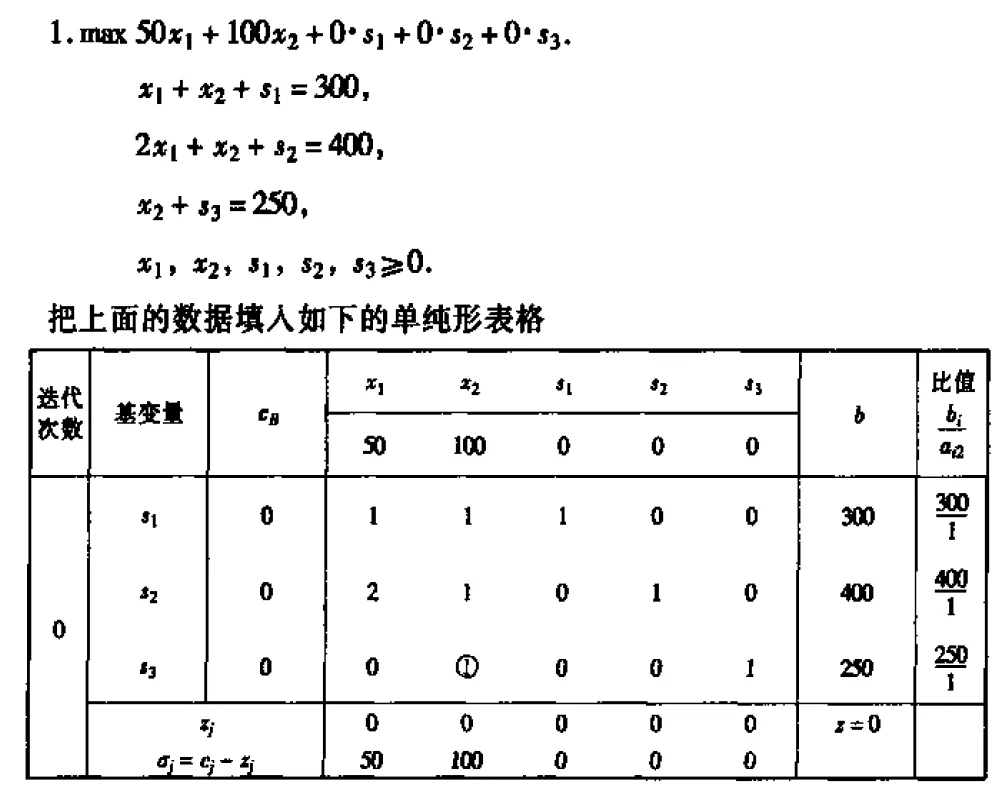
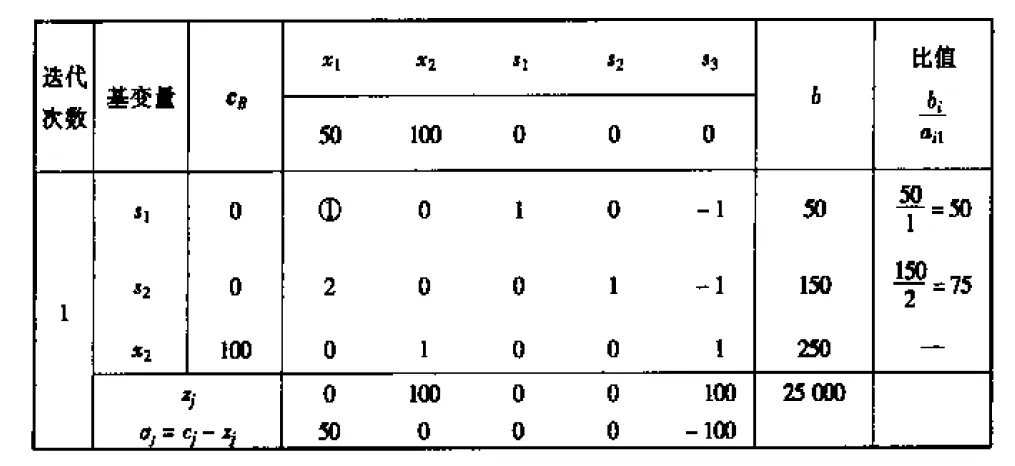
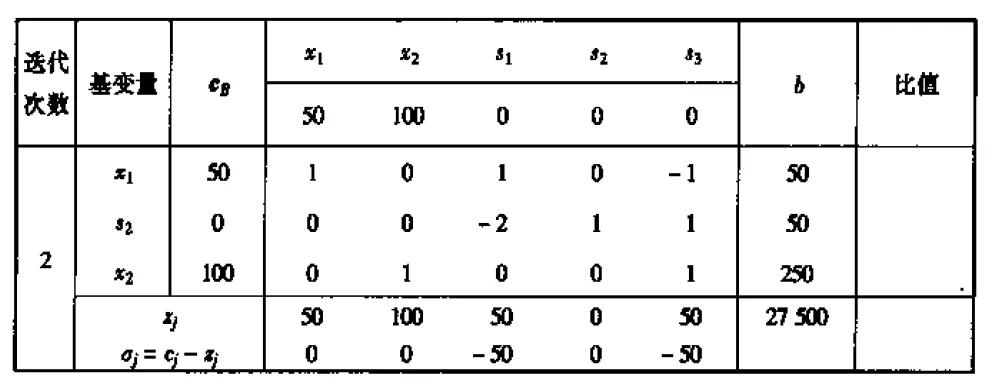
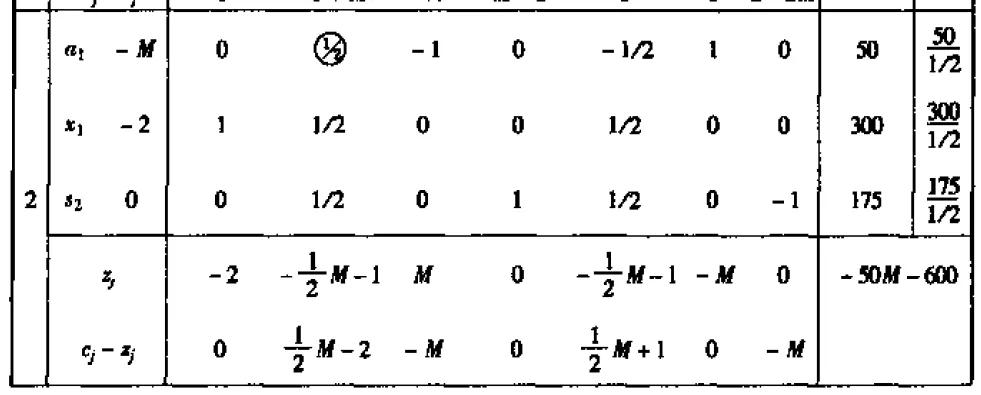
上面用圈圈住的的$a_{ij}$表示的是出基变量和入基变量的行列交叉系数。
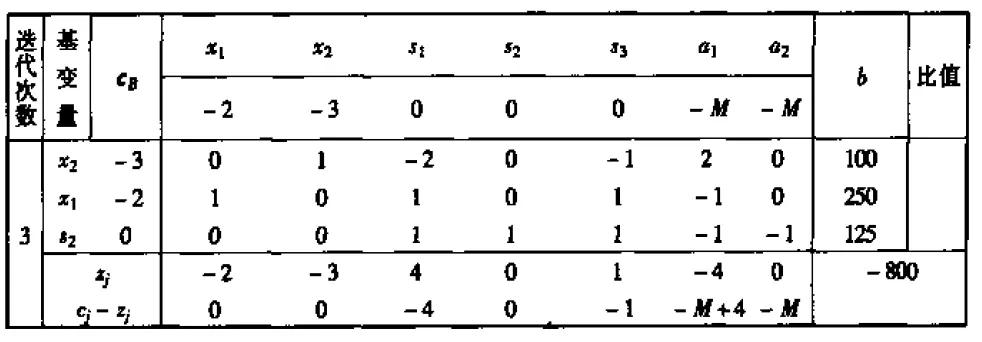
最后一个迭代步骤的结果，得到的检验数都小于等于 0，说明到了最优的情况了。

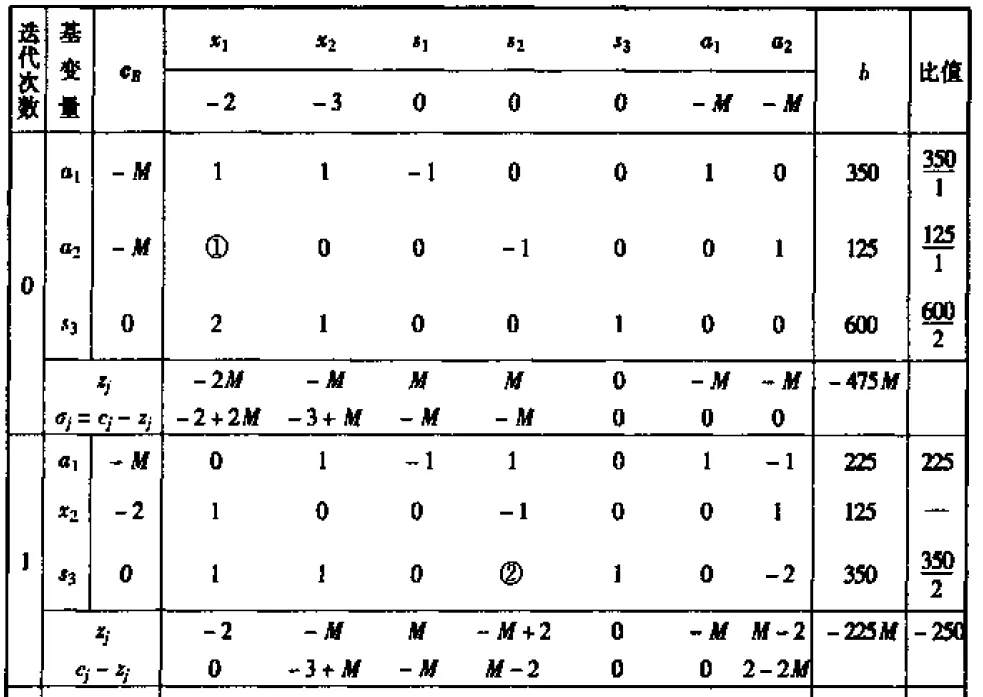
求目标函数值最小的线性规划问题：

1. 大 M 法
我们通常将目标函数值最小的问题转换为目标函数值最大的问题来进行求解， 但转换后的约束方程组中可能找不到单位矩阵，这时候就要添加正的人工变量，拼凑 出单位矩阵，然后对于人工变量，我们要求将他们尽早出基，于是便在目标函数中， 添加一个$-M$系数，$M$为一个尽可能大的数。这样使得它们对于目标函数有尽量大的 负面影响。

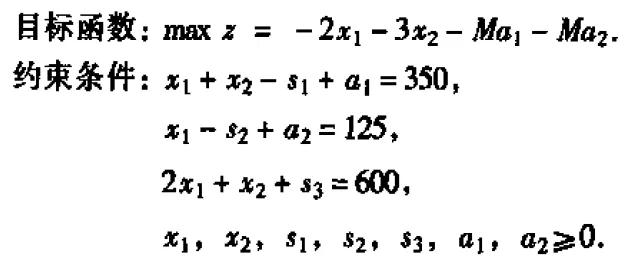
2.两阶段法
第一阶段： 判断原线性规划问题是否有基本可行解：
这个步骤通过求解人工变量的相反数的最大值为目标，若该值小于 0，则说明无解，若 该值等于 0，则说明存在可行解，可以继续求解。
第二阶段： 使用上一阶段的最后一次迭代过程的可行解作为初始可行解继续迭代求解。

几种特殊情况：
1.无可行解
2.无界解
3.无穷多最优解
4.退化问题

单纯形法的灵敏度分析与对偶

单纯形表的灵敏度分析

一、目标函数中变量系数$c_K$的灵敏度分析

1. 在最终的单纯形表中，若$x_K$是非基变量

当$c_K$变成$c_K+\Delta c_K$时，最终单纯形表中的增广矩阵不变。 因为$x_K$是非基变量，所以，目标函数的基变量系数$c_B$不变， 所以可知$z_K$不变。因此变化后的检验数为$\sigma_K+\Delta z_K=c_K+\Delta c_K-z_K$。 要使最优解不变，则要$\sigma_K+\Delta z_K \le 0$。所以有$\Delta z_K \le -\sigma_K$。 2. 在最终的单纯形表中，若$x_K$是基变量

当$c_K$变成$c_k+\Delta c_k$时，最终单纯形表中的增广矩阵不变。 但基变量在目标函数中的系数$c_B$变了，所以$z_j$也变了，所以检验数也变了。

设$c_B'=(c_{B1},c_{B2},...,c_{BK}+\Delta c_K,...,c_{Bm})$,$a_{mj}=(a_{1j},a_{2j},...,a_{mj})$，有:

$z_j=c_B \times a_{mj}^T=c_{B1}a_{1j}+...+c_{BK}a_{kj}+\Delta c_ka_{kj}+...+c_{Bm}a_{mj}=z_j+\Delta c_Ka_{kj}$

这样检验数就变成了$\sigma_j(j=1,2,...,m)$变成了$\sigma'_j$，有：

$\sigma'_j=c_j-z'_j=c_j-(z_j+\Delta c_ka'_{kj})=(c_j-z_j)-\Delta c_ka'_{kj}=\sigma_j-\Delta c_ka'_{kj}$

要使最优解不变，

当$j \ne k$时，$\sigma'_j \le 0$，也就是：

$\sigma_j - \Delta c_k a'_{kj} \le 0$ $\Delta c*k a'*{kj} \ge \sigma_j$

当$a'_kj > 0$ 时，$\Delta c_j \ge \frac {\sigma_j}{a'_{kj}}$，这里$\frac{\sigma_j}{a'_{ij}} \le 0$；

当$a'_kj < 0$ 时，$\Delta c_j \le \frac {\sigma_j}{a'_{kj}}$，这里$\frac{\sigma_j}{a'_{ij}} \ge 0$.

而当$j=k$ 时，因为$a'_{kk} = 1 , \sigma_k = 0$, 所以 $\Delta c_j = 0.$

综上: $max \{\frac{\sigma*j}{a'*{kj}} | a'_{kj}\} \le \Delta c_k \ge min \{ \frac {\sigma_j}{a'_{kj}} | a'\_{kj} \}.$

约束方程中常数项的灵敏度分析

约束方程中常数项的变化不会影响基变量的选择，只会影响基变量的值。
假设基变量$x_k$的常数项$b_k$变化了$\Delta b_k$:
我们有基变量：
$\boldsymbol{x'_B} = \boldsymbol{x_B} + B^{-1}\Delta b_k = (x_{B1},...,x_{Bn})^T + (\Delta b_k b'_{1k},...,\Delta b_k b'_{mk})^T$ 对偶价格：
常数项增加一单位，对目标的影响程度称为对偶价格，在单纯形表中体现为$z_i$。
影子价格：
对于剩余变量而言，常数项增加一单位，对目标有恶化作用，恶化程度称为影子价格，是对偶价格的相反数。

通过要求最优解的大于等于 0 约束得到：
$max\{ -\frac{x*{Bi}}{d'*{ik}} | d'_{ik} \lt 0 \} \le \Delta b_k \le min \{- \frac{x_{Bi}}{d'_{ik}} | d'_{ik} \lt 0 \}.$

系数矩阵 A 的灵敏度分析

1. 若迭代后的系数向量为非基变量的向量：
   只要 $\sigma'_k = c_k - z_k = c_k - c_BB^{-1}p'_k \le 0$ 就不会产生基变量的变化，因此只 要计算这个数值是否满足条件就好了；

2. 若迭代后的系数向量为基变量的向量：
   这时问题会变得很复杂，最优解的可行性和最优解都有可能遭到破坏，因此一般不去修改最终表，而 是重新计算。

增加一个约束条件的灵敏度分析

先将原最优解带入新的约束条件中，若满足，则该约束条件不起作用，最优解不变；将新约束条件添 入最终单纯形表中进一步求解。

对偶问题写法

要点：

1. max -> min
2. n 个变量 m 个约束 -> m 个变量 n 个约束
3. 系数矩阵$A \rightarrow A^T$
4. 约束条件大于变成小于
5. 目标函数系数变为原问题的常数项
6. 常数项变为原问题的目标函数系数项
7. 原问题没有非负限制的变量，对偶问题中对应的约束条件要变成等号
8. 原问题中约束条件为等号的，对偶问题对应的变量要变成无限制

对偶规划的基本性质

1. 对称性
2. 弱对偶性
3. 最优性
4. 强对偶性
5. 互补松弛性